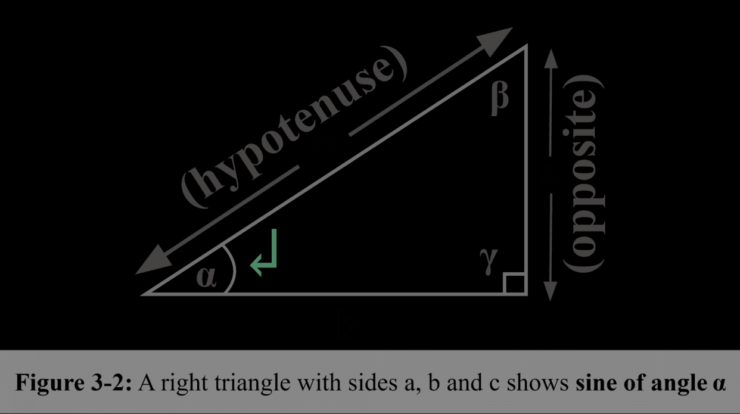
Sine definition – Embarking on a journey into the realm of trigonometry, we encounter the enigmatic sine function, a fundamental concept that unlocks a world of mathematical possibilities. Sine, a trigonometric function, holds the key to understanding the intricate relationships between angles and sides in triangles, making it an indispensable tool in various scientific disciplines.
Delving deeper into its mathematical essence, sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle. This ratio provides a numerical value that quantifies the relationship between the angle and the triangle’s dimensions.
Sine: A Trigonometric Function
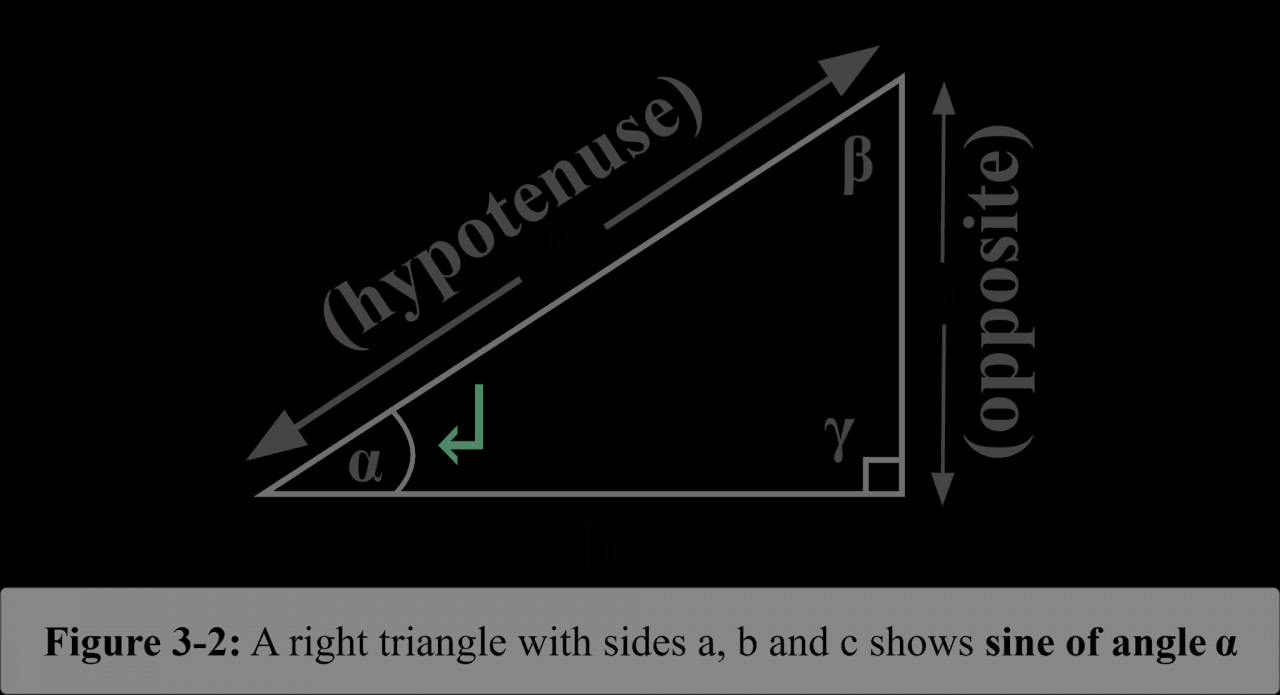
Sine is a fundamental trigonometric function that plays a crucial role in mathematics and various scientific fields. It is defined as the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse.
The formula for calculating sine is:
sin(θ) = opposite/hypotenuse
where θ represents the angle in question.
Graph and Properties
The graph of the sine function is a periodic curve that oscillates between -1 and 1. It has a period of 2π, meaning that it repeats itself every 2π units along the x-axis.
Key features of the sine graph include:
- Amplitude: 1 (the distance from the midline to the maximum or minimum value)
- Period: 2π (the distance between two consecutive peaks or troughs)
- Phase shift: 0 (the horizontal shift of the graph from its standard position)
The sine function also exhibits properties such as periodicity (it repeats itself after a certain interval) and symmetry (it is odd, meaning it is symmetric about the origin).
Applications in Trigonometry, Sine definition
Sine is used extensively in trigonometry to solve equations and find angles and distances in triangles. For instance, it is used to calculate the angle of elevation or depression when an observer is at a known distance from an object.
Additionally, sine is used to calculate trigonometric ratios, such as cosine and tangent, which are essential for solving a wide range of trigonometric problems.
Applications in Physics and Engineering
Sine has numerous applications in physics and engineering. In physics, it is used to describe wave motion, including the motion of sound waves and light waves.
In engineering, sine is used in the design and analysis of structures such as bridges and buildings. It is also used in acoustics to analyze sound waves and in electrical engineering to analyze alternating current circuits.
Final Review: Sine Definition
In conclusion, sine definition forms the cornerstone of trigonometry, providing a powerful tool for solving a myriad of problems in mathematics, physics, and engineering. Its versatility and wide-ranging applications make it an essential concept in the exploration of the natural world and beyond.
Question & Answer Hub
What is the formula for sine?
Sine is calculated as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle: sin(θ) = opposite/hypotenuse.
What is the range of the sine function?
The range of the sine function is between -1 and 1, inclusive.
What are the key features of the sine graph?
The sine graph is a periodic function with an amplitude of 1, a period of 2π, and a phase shift of 0.





